In this complete example, we seek to maximize revenue by determining the optimal number of baked goods to produce, from a limited selection of ingredients and so on. Each product requires a selection of ingredients, and each ingredient has a maximum available amount that we cannot exceed.
Step 1: Prepare the data (Model)
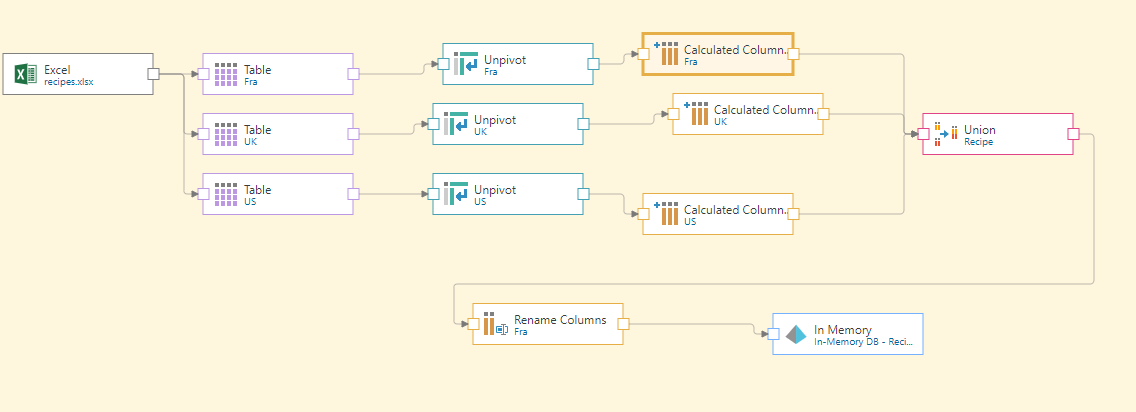
- First, we copy the information that we have into Excel. We create separate sheets with slightly different quantities, to replicate different demands from different markets. We have one of these sheets representing the UK, one the US, and one representing France.
- We import this spreadsheet into Pyramid, taking each of the separate sheets as a separate Pyramid table. The basic model is as follows:

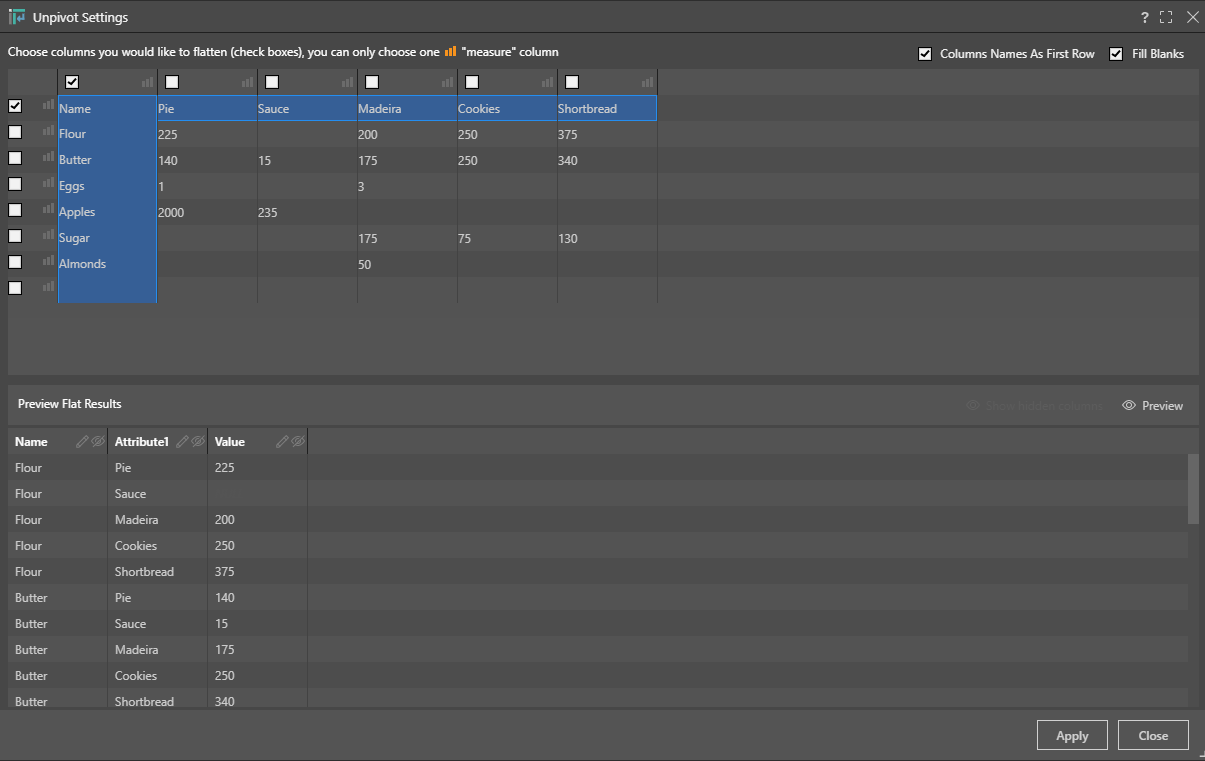
- To convert the tables to the correct format for Pyramid, we use Unpivot nodes to flatten the columns:
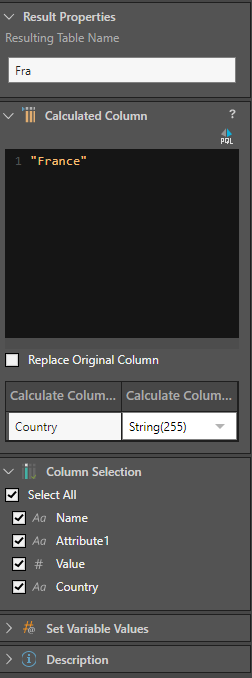
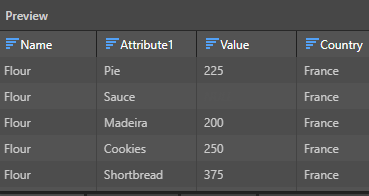
- We next use Calculated Column nodes to add a "Country" column, to associate a country with all the data. We will later use this to filter the displayed data by country:
- We must rejoin the tables, using a Union node.
- Finally, before we run the model, we rename the columns with more sensible names, using the Rename Columns node:
The final model looks like this:
Step 2 - Build Model and Run Discovery
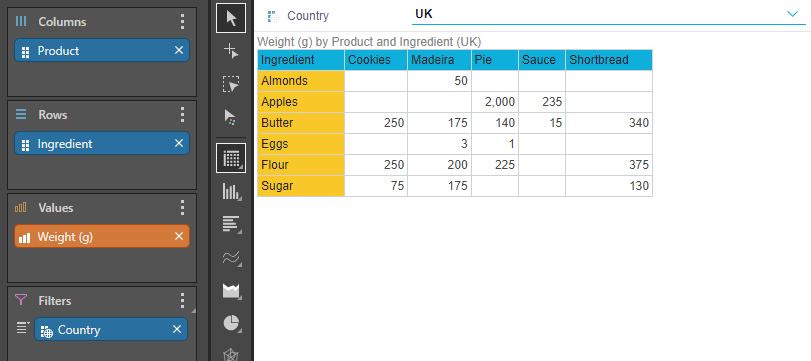
- Building this model and running a new Discovery gives us the following:
- We have introduced a slicer, so we can display the spreadsheet for a specific country. We also add the other data specified, which Solve needs to perform its calculations:
- Note: As well as the stated data, we must also enter a set of values for "Amounts to Produce", which have been entered in cells R3 to R7. These are the decision variables, whose value we can change so as to maximize the "Total Revenue" (cell U2), which is defined as the sum of the numbers of the different products to be baked, multiplied by the profit for each one (the values in cells O3 - O7). The formula for the revenue cell, U2, is

=SUMPRODUCT(R3:R7,O3:O7)
Step 3 - Configure and Run Solve
- From the ribbon at the top of the page, click Advanced Settings > Solve (green).
- Specify the Optimization Objective as follows:
-
Enter the constraints information from the Constraints section of the grid. All constraints of the same type can be included in one instruction in the Solve panel. In our example, the values in cells K7 to K12 (quantities used) cannot be greater than the values in cells L7 to L12 (maximum quantities available). Here, we have also introduced a constraint that we must have at least six of each item (cells R3 to R7 must all have a value of at least 6):

Note: The Solve button is only shown on this Tabulate ribbon if your profile enables Solve. For more information, see Pro User Profile.
The Solve panel opens at the bottom of the Tabulate page. The Equations tab is open by default.
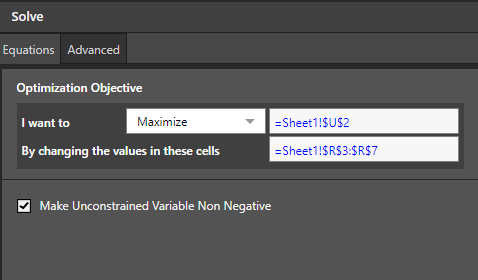
Note: You are trying to maximize the value in your revenue cell, this is cell U2 of your sheet (Sheet1). The variables that will effect this cell are found in cells R3 to R7 of the same sheet (these cells define the Amounts to Produce).

Finally, click Apply or Apply and Close to run the optimization.
Outcome
The details of the optimization are given in the Results List in the Solve panel.
The actual results are displayed in the spreadsheet, which shows the optimal amount of each product to bake, the amount of the different ingredients used, and the resulting revenue:
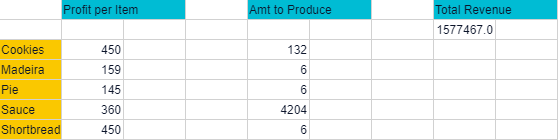
So, Solve has determined that the optimal revenue is obtained by producing the following, given the figures supplied:
-
sauce (4,204 bottles)
-
cookies (132)
If we amend the details, Solve recalculates the optimal solution. So, for example, if we double the amount of butter used in the sauce, to 30g, and increase the amount of sugar in the cookies to 100g, (assuming that a different market has different tastes), and run Solve again, the solution changes to suggest that we should stick to producing mainly sauce - 3,152 bottles, with minimum quantities of everything else. This produces a decreased revenue of 1,142,064, which is optimal given the new circumstances.
On the other hand, suppose we again have 30g of butter in the sauce, but this time increase the amount of butter in the cookies too, to 300g, instead of increasing the sugar; here, again, the optimal solution that Solve suggests produces mainly sauce, with minimum quantities of everything else. However, now we are producing less sauce (3,142 bottles), and have a correspondingly reduced revenue of 1,138,464.