The advanced options are used to specify and constrain the particular method used when optimizing the objective value. These options let you adjust the settings used by the algorithm to find more appropriate or otherwise better results. If you need more information about Solve before you begin, see Solve Overview.
- This panel is opened by clicking the Advanced tab (red arrow) in the Solve panel.
For more information about general options on the Equations page, and how to open the Solve panel, see: Solve Panel.
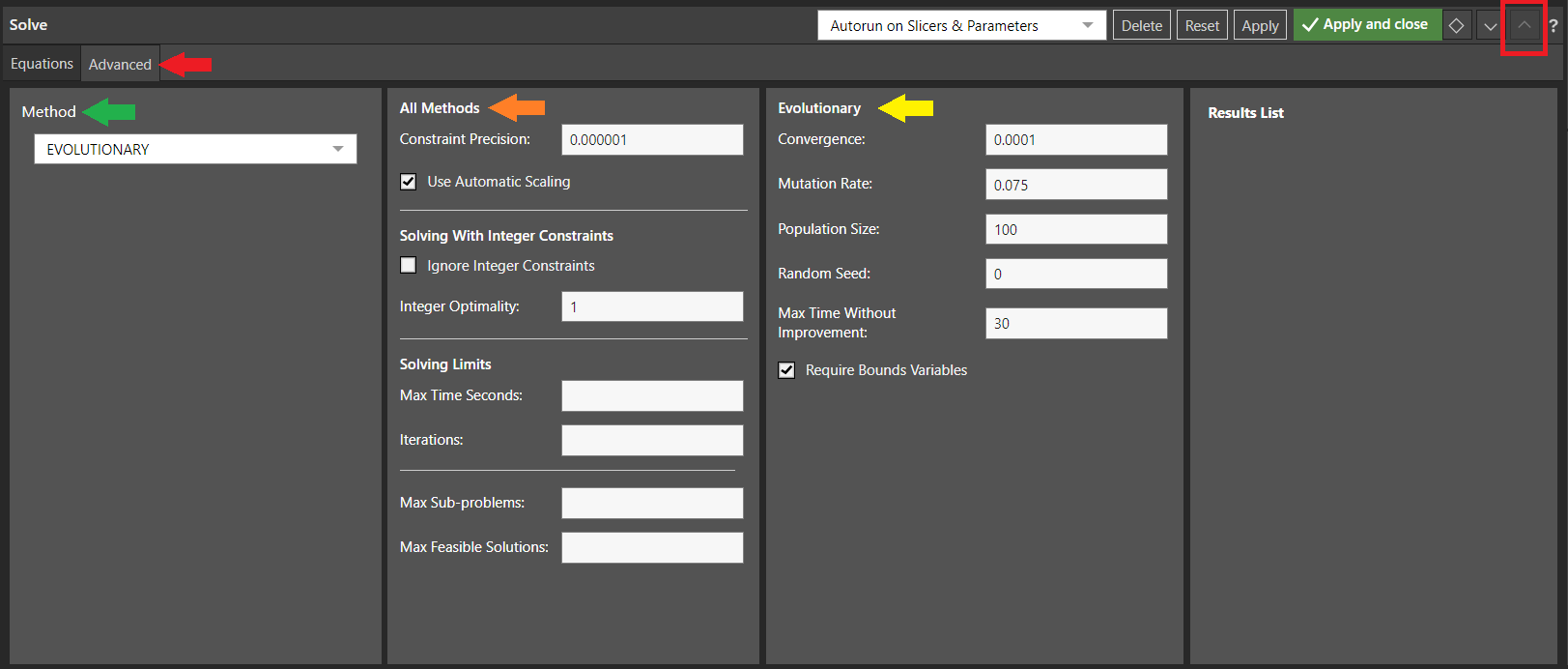
Tip: The preceding screen shot shows the Solve panel in its Maximized state (red box). When you are working on Advanced Settings, you might find maximizing the panel helpful.
Select a Solver Method
When you configure the advanced settings in Solve, you indicate which method you want to use to create your optimizations, and configure how the underlying Solver should behave by tweaking the standard settings (All Methods) or the settings that are applicable to your selected method (Method-Specific).
You can select the Method that you want to use in the Method panel (green arrow), the options are as follows:
- Auto Detect: Allow Solve to automatically select the best method to use, given your basic settings.
- Simplex LP: Select to use the Simplex LP Solver Pro to resolve linear problems.
- GRG Nonlinear: Select to use the nonlinear GRG Solver to resolve smooth nonlinear problems.
- Evolutionary: Select to use the Evolutionary Solver to resolve non-smooth problems.
Once you have made your selection, you can further configure the Solver using the settings in the All Methods panel and, if you have selected GRG or Evolutionary, the Method Specific panel.
Select Simplex LP in the Method panel to use the Simplex LP Solver Pro method to resolve linear problems.
The Simplex method finds optimal solutions to problems where the objective and constraints are all linear functions of the variables. Since all linear functions are convex, the Solver can normally find the globally optimal solution, if one exists. Because a linear function (a straight line) can always be increased or decreased without limit, the optimal solution is always determined by the constraints.
Select GRG Nonlinear in the Method panel to use the GRG Solver to resolve smooth nonlinear problems.
The nonlinear GRG Solver finds optimal solutions to problems where the objective and constraints are all smooth (convex or nonconvex) functions of the variables. (You can imagine a graph - whether straight or curved - that contains no "breaks".) For non-convex problems, the Solver normally can find a locally optimal solution, if one exists - but this may or may not be the globally optimal solution. A nonlinear objective function can have a natural "peak" or "valley", but in most problems the optimal solution is partly or wholly determined by the constraints. The nonlinear GRG can be used on problems with all-linear functions, but it is much less effective and efficient than the LP Solver on such problems. If you use multi start methods for global optimization with the nonlinear GRG, you will have a better chance (but not a guarantee) of finding the globally optimal solution. The idea behind multi start methods is to automatically start the Solver from a variety of starting points, to find the best of the locally optimal solutions - ideally the globally optimal solution.
Use to resolve non-smooth problems. The Evolutionary Solver usually finds good solutions to problems where the objective and constraints include non-smooth or discontinuous functions of the variables - in other words, where there are no restrictions on the formulas that are used to compute the objective and constraints. For example, if your model uses IF, LOOKUP, or similar functions of the variables, it's likely that the graphs of these functions will contain "jumps" or "breaks". For this class of problems, the Solver will return the best feasible solution (if any) that it can find in the time allowed. The Evolutionary Solver can be used on problems with all-smooth functions that may have multiple locally optimal solutions, in order to seek a globally optimal solution, or simply a better solution than the one found by the nonlinear GRG Solver alone. It can be used on problems with smooth convex functions, but it is usually less effective and efficient than the nonlinear GRG Solver on such problems. Similarly, it can be used on problems with all-linear functions, but there is little point in doing so when the Simplex Solver is available.
All Methods panel
The All Methods settings are applicable to any of the methods that Solve might use to resolve the problem and create the optimization:
|
Field |
Description |
|---|---|
|
Constraint Precision |
The required degree of precision. For a constraint to be considered satisfied, the relationship between the Cell Reference and the Constraint value cannot be violated by more than this amount. The smaller the number, the higher the precision. |
|
Use Automatic Scaling |
Internally rescale the values of variables, constraints, and the objective to similar magnitudes. This reduces the impact of extremely large or small values on the accuracy of the solution process, and is enabled by default. |
"Solving with Integer Constraints" options
|
Field |
Description |
|---|---|
|
Ignore Integer Constraints |
Ignore the integer, binary, and all different constraints when you run Solve. Note: This is called solving the relaxation of the integer programming problem. |
|
Integer Optimality |
The maximum percentage difference between the objective value of the best integer solution and the best known bound-on true optimal objective value that Solve should accept before stopping. The default value is 1%. Set to 0% to ensure a proven optimal solution is found. Note: The Integer Optimality percentage is sometimes called the (relative) "MIP gap". |
"Solving Limits" options
|
Field |
Description |
|---|---|
|
Max Time Seconds |
The maximum time, in seconds, that Solve runs for before it stops. |
|
Iterations |
The maximum number of iterations that Solve may perform on one problem. Iterations are "pivots" for the Simplex method, or "major iterations" for the GRG method. |
|
Max Sub-problems |
The limit on the number of sub-problems explored by the Branch & Bound algorithm before Solve stops. |
|
Max Feasible Solutions |
The limit on the number of "candidate" integer solutions found by the Branch & Bound algorithm before Solve stops. |
Method-Specific panel
The Method-specific panel contains different options depending on the selected method type. The following details describe the settings in this panel, and which method they are applicable to.
Note: The yellow arrow in the preceding example shows the options where the Evolutionary method is selected.
|
Field |
Method |
Description |
|---|---|---|
|
Convergence |
GRG Nonlinear; Evolutionary |
The amount of
relative change allowed in the last five iterations before Solve
stops with the message Note: Providing smaller values typically means that Solve will take more time but stop at a point closer to the optimal solution. |
|
Derivatives |
GRG Nonlinear only |
Select the mechanism to use to estimate derivatives:
|
|
Mutation Rate |
Evolutionary only |
A number between 0 and 1 that indicates the relative frequency with which some member of the population will be altered or "mutate" to create a new trial solution during each generation or sub-problem considered by the Evolutionary method. A higher Mutation Rate increases the diversity of the population and the chance that a new, better solution, will be found; but may also increase the total solution time. |
|
Use Multi start |
GRG Nonlinear only |
Use the multi start method for global optimization. If this option is selected when you run Solve, the GRG Nonlinear method is run repeatedly, starting from a different (automatically chosen) starting value for the decision variable. This process may find a better solution, but will take more computing time than a single run of the GRG Nonlinear method. |
|
Population Size |
GRG Nonlinear; Evolutionary |
The number of different starting points (values for the decision variables) for the method to consider:
|
|
Random Seed |
GRG Nonlinear; Evolutionary |
The random seed for the random number generator used when creating candidate starting points for your selected method. The seed number entered here is used as a fixed starting point for the random number generator:
|
|
Maximum Time without Improvement |
Evolutionary only |
The maximum number of seconds you
want the Evolutionary method to continue for without a meaningful improvement in
the objective value of the best solution in the population. After this time,
Solve will stop with the message |
|
Require Bounds Variables |
GRG Nonlinear; Evolutionary |
The method will only run if there are lower and upper bounds defined on all decision variables with Constraints. Note: The method is far more effective if bounds are defined on all variables. The tighter the bounds on the variables, the better the method is likely to perform. |
Other Topics
- For details of the step-by-step process that you need to follow to open Solve and find an optimization, see Open Solve and Create an Optimization.
- For a full end-to-end walkthrough of an example Solve optimization, see Complete Solve Example.